Dot Product of Two Vectors
Mathematically angle α between two vectors can be written as. Let θ be the angle between them.

Product Of Vectors Vector Multiplication Vector Can
The main attribute that separates both operations by definition is that a dot product is the product of the magnitude of vectors and the cosine of the angles between them whereas a cross product is the product of magnitude of vectors and the sine of the angles between them.

. There are two vector A and B and we have to find the dot product and cross product of two vector array. The full version. Find the dot product of two or more vectors with an equal number of terms.
But the most commonly used formula for finding an angle between two vectors involves the scalar product. For vectors a a 1 a 2 a 3 and b b 1 b 2 b 3the dot product can be found by using the following formula. Result of dot product in the form of Matrix Product.
In mathematics an inner product space or rarely a Hausdorff pre-Hilbert space is a real vector space or a complex vector space with an operation called an inner product. Two types of multiplication involving two vectors are defined. The scalar triple product of three vectors is defined as Its value is the determinant of the matrix whose columns are the Cartesian coordinates of the three vectors.
Now if two vectors are orthogonal then we know that the angle between them is 90 degrees. To calculate the angle between two vectors in a 2D space. Calculate the magnitude of both the vectors separately.
Characters other than numbers are not accepted by the. And press Calculate the dot Product. A vector has both magnitude and direction.
Use of Dot Product Calculator. Cross product is a form of vector multiplication performed between two vectors of different nature or kinds. In this article we would be discussing the dot product of vectors dot product definition dot product formula and dot product example in detail.
The answer is a scalar. Divide the resultant by the magnitude of the second vector. We can multiply two or more vectors by cross product and dot productWhen two vectors are multiplied with each other and the product of the vectors is also a vector quantity then the resultant vector is called the cross.
Therefore two perpendicular vectors will have a dot product of zero. Where i j and k are the unit vector along the x y and z directions. I was wondering if a dot product is technically a term used when discussing the product of 2 vectors is equal to 0.
A vector has magnitude how long it is and direction. The overdot notation I used here is just a convenient way of not having to write out. Find the dot product of the vectors.
The inner product of two vectors in the space is a scalar often denoted with angle brackets such as in Inner products allow formal definitions of intuitive geometric notions such as lengths angles and. We can calculate the dot product for any number of vectors however all vectors must contain an equal number of terms. They can be multiplied using the Dot Product also see Cross Product.
Dot Product Let we have given two vector A a1 i a2 j a3 k and B b1 i b2 j b3 k. Magnitude can be calculated by squaring all the components of vectors and adding them together and finding the square. A b 1-2 -21 -2.
The scalar product of two vectors is equal to the product of their magnitudes. Given vectors u v and w the scalar triple product is uvXw. The Dot Product is written using a central dot.
Dot product is also known as scalar product and cross product also known as vector product. α arccosx a x b y a y b x a 2 y a 2 x. So if we take two vectors one has to be written in the form of row matrix and the other in the form of column matrix.
The so-called scalar product or dot product and the so-called vector product or cross product. The angle between vectors can be found by using two methods. While this is the dictionary definition of what both operations mean theres one major characteristic.
BeginarraylvecAvecB A_xB_x A_yB_yA_zB_zendarray Step 2. Evaluate the determinant youll get a 3 dimensional vector. Note that the angle between the two vectors remains between 0 and 180.
A b This means the Dot Product of a and b. The dot product of two different vectors that are non-zero is denoted by ab and is given by. And would anyone agree that an inner product is a term used when discussing the integral of the product of 2 functions is equal to 0.
We can calculate the Dot Product of two vectors this way. Here are two vectors. It is the signed volume of the parallelepiped defined by the three vectors and is isomorphic to the three-dimensional special.
Angle Between Two Vectors in 2D Using Dot Product. 1 - Enter the components of the two vectors as real numbers in decimal form such as 2 15. So by order of operations first find the cross product of v and w.
Divide the dot product by the magnitude of the first vector. It can be obtained using a dot product scalar product or cross product vector product. Let us find the angle between vectors using both and dot product and cross product and let us see what is ambiguity that a cross product can cause.
Let us compute the dot product and magnitudes of both vectors. This physics and precalculus video tutorial explains how to find the dot product of two vectors and how to find the angle between vectors. You will notice many science books or research papers where dot products are written as the product of row and column matrix.
Find a b when a and b a b. Or is there no difference at all between a dot product and an inner product. An online calculator to calculate the dot product of two vectors also called the scalar product.
Calculate the dot product of two given vectors by using the formula. The dot product gives us a very nice method for determining if two vectors are perpendicular and it will give another method for determining when two vectors are parallel. This dot product is widely used in Mathematics and Physics.
A b a 1 b 1 a 2 b 2 a 3 b 3. Note as well that often we will use the term orthogonal in place of perpendicular. Ab ab cos θ.
There are two ternary operations involving dot product and cross product. For simplicity we will only address the scalar product but at this point you should have a sufficient mathematical foundation to understand the vector product as well. Set up a 3X3 determinant with the unit coordinate vectors i j k in the first row v in the second row and w in the third row.
Begingroup It merely sounds to me that youre unfamiliar with vector calculus versions of the product rule but they are no more exotic than the single-variable version and follow directly from that version which can be proved by breaking into components if you insist.

Dot Product Explained Vector Calculus Calculus Mathematics Geometry
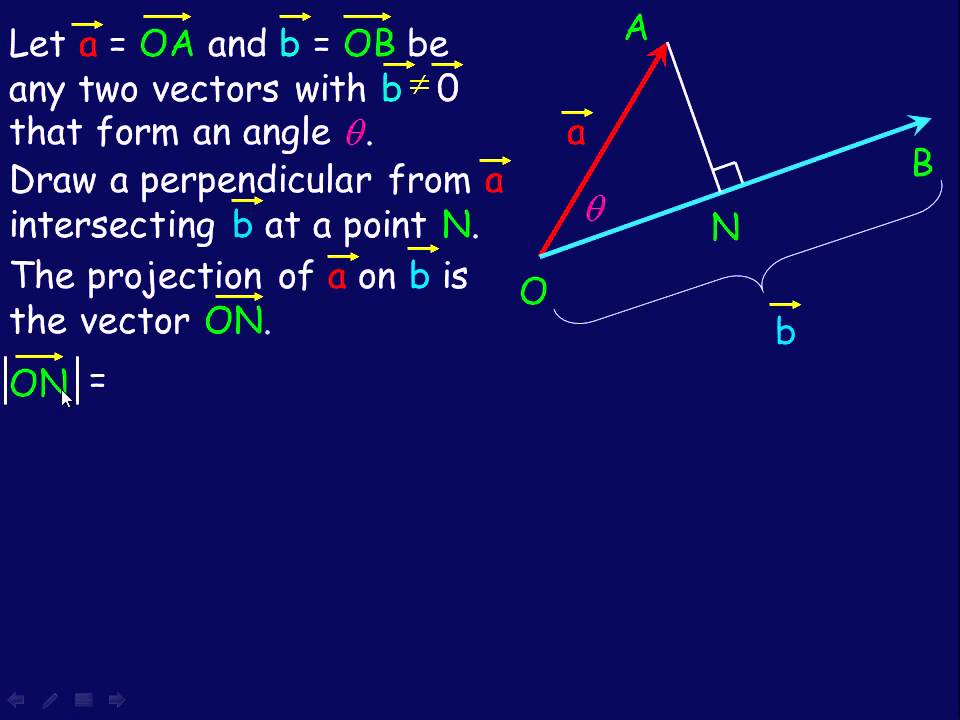
Applications Of The Dot Product Avi Calculus Mathematics 12th Maths

How To Memorize Things Commutative Vector

How To Find The Scalar And Vector Product Of Two Vectors Easily How T Mathematics Vector Math

Dot Product A Plus Topper Reciprocalsystemofvectors Dots Commutative Positivity

Dot Product A Plus Topper Reciprocalsystemofvectors Dots Positivity Commutative
0 Response to "Dot Product of Two Vectors"
Post a Comment